Monotonic Neural Network

There are many situations when one would like to recover a monotonic functions from (noisy) data. For example, in a regression setting, that is usually called an isotonic regression model. This can be useful, for example, when modeling a relationship of the type (happiness) ~ F(income) for some unkown function F that one can quite safely assume monotonic increasing.

How do we build a neural architecture such that, for any set of neural weights $^{}$ the neural network represents a function $F_{}: ^d$ that is increasing along any of the $d$ coordinates? That is an old problem, and there are quite a few solutions apparently. For example, I will describe here the basic approach of this 1997 paper (1) by J. Sill.

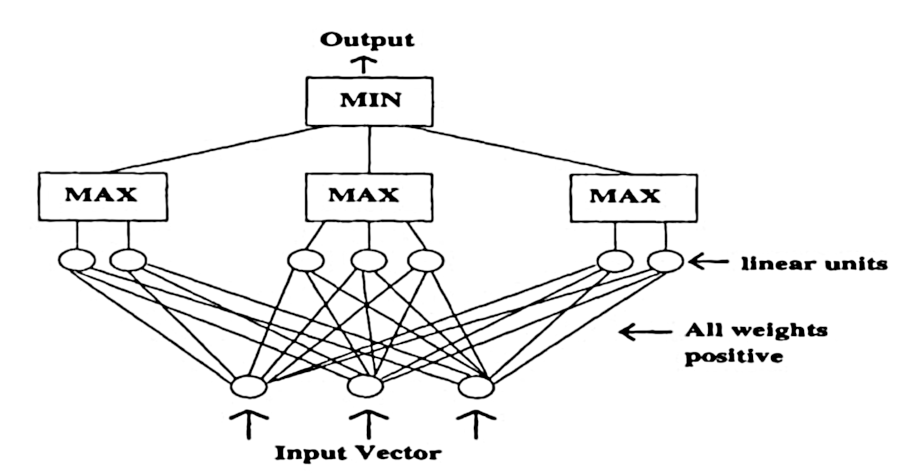
It is based on the fact that if $f_1(x), f_2(x), , f_K(x)$ are $K$ increasing and continuous functions, then so are their pointwise minimum and pointwise maximum. In other words, the two functions $m(x)$ and $M(x)$ defined as

${\displaystyle m(x)={\mathbf{m}\mathbf{i}\mathbf{n}}_{k=1}^K{f}_k(x)}$

and

${\displaystyle M(x)={\mathbf{m}\mathbf{a}\mathbf{x}}_{k=1}^K{f}_k(x)}$

are also both increasing and continuous functions. To construct an “increasing” neural architecture, one can consequently try to build $K$ relatively simple increasing functions $f_1(x), , f_K(x)$ and define the output of the neural network as their minimum,

${\displaystyle F(x)={\mathbf{m}\mathbf{i}\mathbf{n}}_{k=1}^K{f}_k(x)\mathrm{.}}$

Now, to construct each one of these simple increasing functions $f_k(x)$, one can choose $G$ vectors with non-negative coordinates $^{k,1}, , ^{k,G} ^d_+$ and biases $b^{k,1}, , b^{k,G}$ and define

${\displaystyle f_k(x)={\mathbf{m}\mathbf{a}\mathbf{x}}_{k=1}^K⟨{\omega }^{k,g},x⟩+b^{k,g}}$

where $u,v = u_1 v_1 + + u_d v_d$ is the usual Euclidean dot-product. To inplement this, one can use a soft-plus operation, i.e. ${k,g} = (^{k,g})$ with no constraint on ${k,g}$, or anything equivalent, to make sure that these weights are nonnegative. Below, I have implemented this with $K=20$ and $G=10$, initialized all the weights randomly from a centred Gaussian with unit variance, and repeated the experiment $100$ times.

Now, we can try to implement a standard regression, but with the constraint that the function is increasing (i.e. isotonic regression). It suffices to minimize the standard Mean Square Error (MSE) with a monotomic neural net. Below shows the dynamics of learning on a simple 1D dataset ${(x_i, y_i)}_{i=1}^N$ and with a standard SGD optimizer.

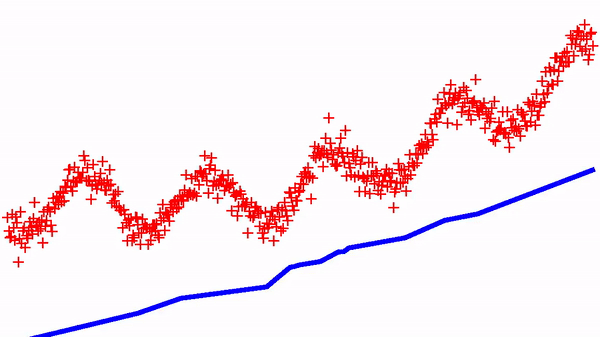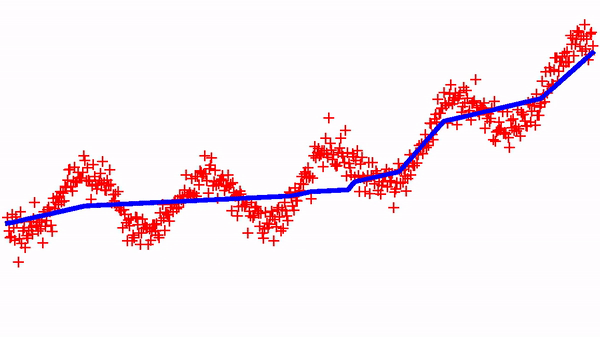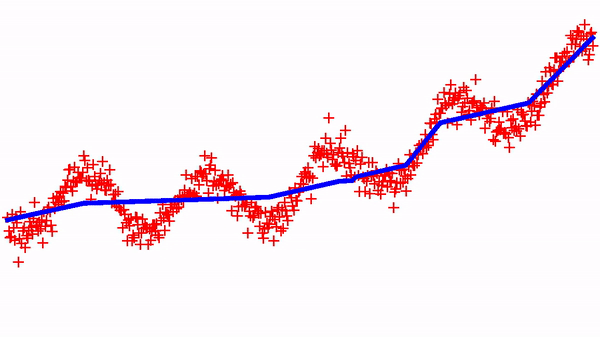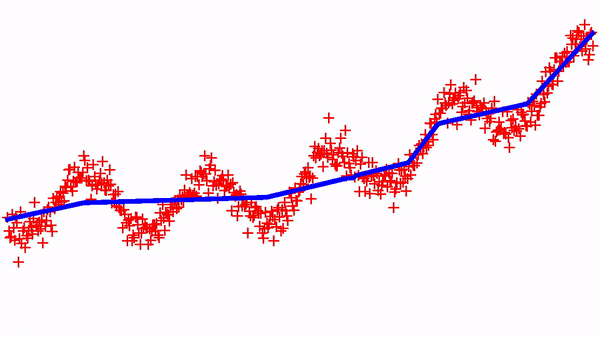
There are variants of this approach for designing neural networks that always represent convex functions — I’ll try to show some simulations in a next blog-post. These monotonic networks are useful in many settings — in a next blog-post, I will use them for implementing a (deep) quantile-regression model…

---

references

1. Sill, J. (1997). Monotonic networks. Advances in neural information processing systems, 10.

---

---

---