Regression with Gaussian Likelihood
In a future post, I would like to implement a (deep) quantile-regression model since I have never tried that before. To warm-up, let us start with a basic Gaussian regression.
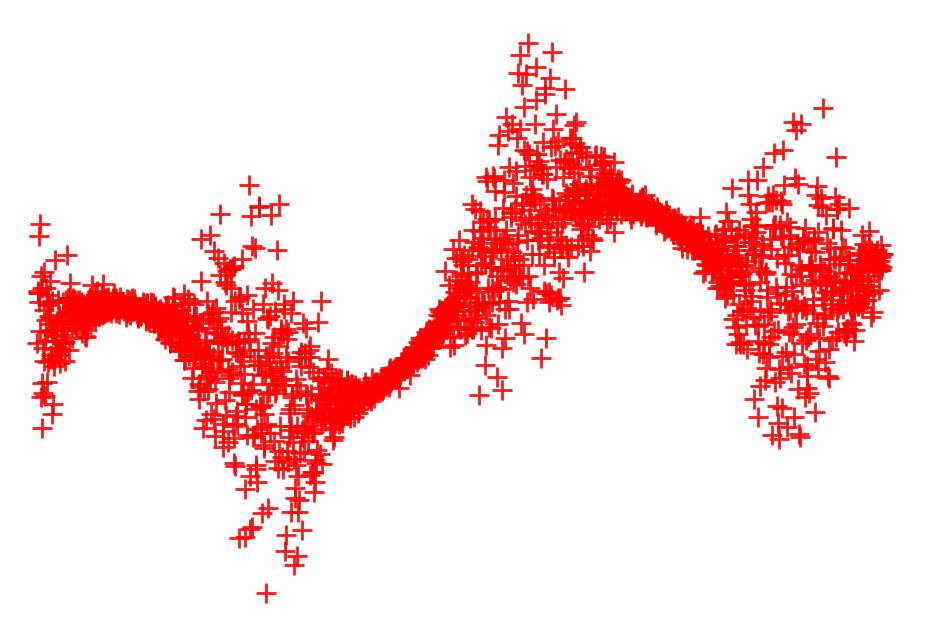
The plot above represents a simple 1D dataset . To build a predictive model, we could simply try to fit a regression of the type
for some unkown function . For implementing this, one could parametrize the function with some parameter (eg. a neural net) and minimize the standard MSE loss,
This simple regression setting does not capture the fact that the uncertainty is much higher at some places than at others. Better would be to use a model of the type
where denotes a Gaussian distribution with mean and variance . Here and are two unkown functions. In other words, one can make the variance term depends on the covariate , and that is the standard approach in this type of situations. Indeed, any other distribution (eg. a Student’s distribution) could be used instead. For implementing this idea, one can use a neural net with parameter that takes as input and spits out the pair . Maximum Likelihood Estimation boils down to minimizing
Using a neural-net with only one hidden layer and a basic SGD optimizer gives the following learning trajectory:
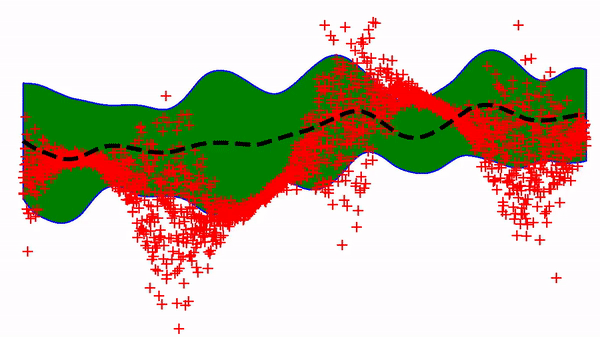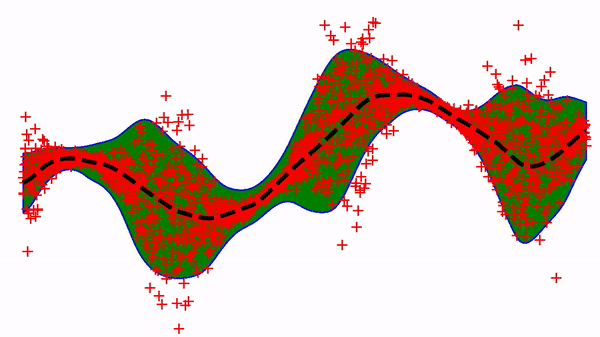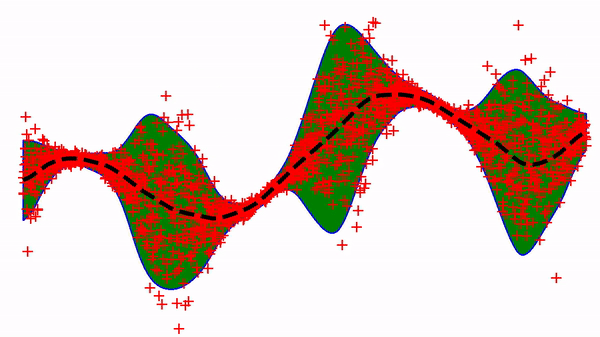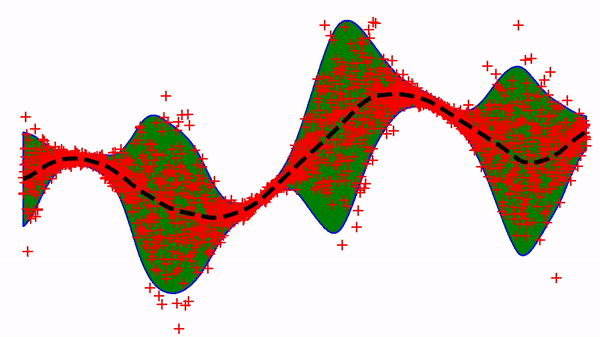
Not bad, although it is known that this simple approach can lead to optimization issues in slightly more complex situations 1,2. For example, it is hard to get out of the local minimum below.
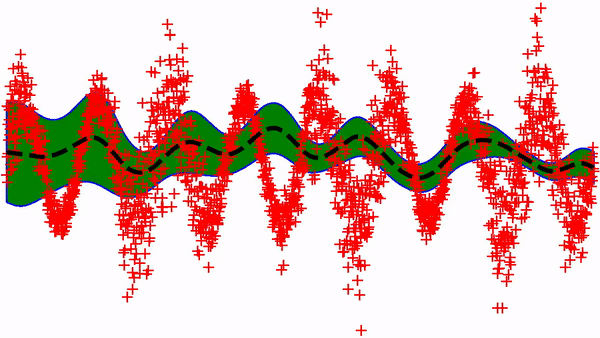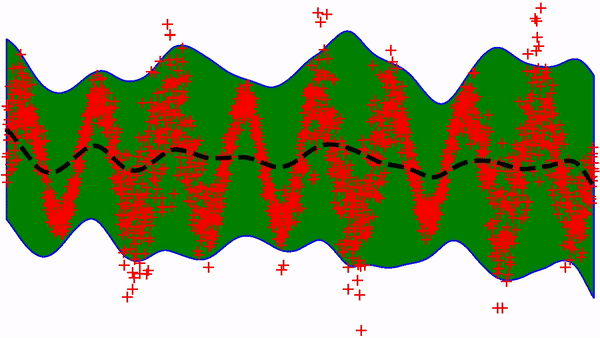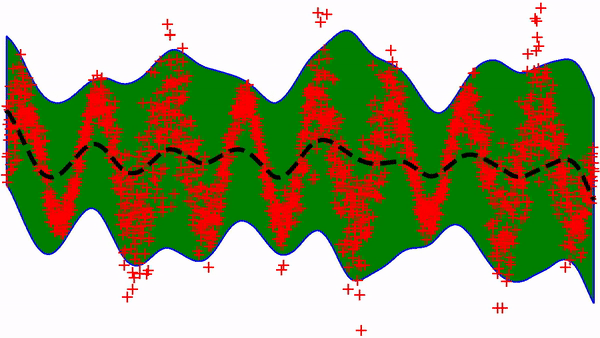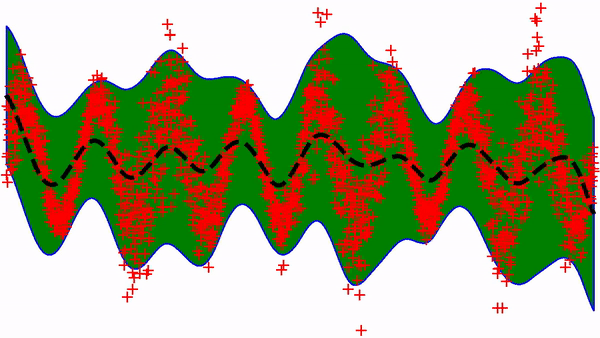
In another post, I’ll try to implement a deep-quantile-regression model…
references
Stirn, A., & Knowles, D. A. (2020). Variational variance: Simple, reliable, calibrated heteroscedastic noise variance parameterization arXiv preprint arXiv:2006.04910.
Skafte, N., Jørgensen, M., & Hauberg, S. (2019). Reliable training and estimation of variance networks Advances in Neural Information Processing Systems, 32.